Ohm’s law is one of the most fundamental laws of electrical science but due to its simplicity it may not be very useful when solving questions regarding complex electrical circuits. A more comprehensive law was needed for this purpose which was put forth by the great German physicist Gustav Kirchhoff and hence the laws are known as Kirchhoff’s laws. Basically they are laws of conservation of charge and electrical energy as applied to electric circuits and are described as follows.

The First Law

Also known by other names such as Kirchhoff’s Current Law and Kirchhoff’s Point Law, it is the law of conservation of charge. It simply states that at any point or junction in an electrical circuit, the total amount of current entering that junction is the same as the total amount of current which leaves that junction.

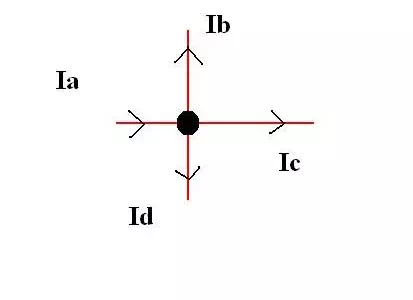
Let us suppose there is an electric circuit which has a point as denoted in figure 1 shown below. The point of the junction acts as a meeting point for four conductors each of which is carrying current in the direction specified as depicted by the black arrow heads. As per the Kirchhoff’s law the sum total of current entering into the junction should be equal to the current going out of it. This can be mathematically represented as follows

Ia = Ib + Ic + Id

Where I is the current in each of the conductors a, b, c and d respectively.

It should also be noted at this point that a capacitor is a device which is used to store charge in the form of electrostatic force in a dielectric material surrounded by conductor plates on both sides. There are some exceptions to the Kirchhoff’s first rule if a capacitor was present in any of the nodes but it is better not to go into such details at this basic level. Hence for all practical purposes in other situations, the Kirchhoff’s rule applies and is valid.

Kirchhoff’s Current Law

The Second Law

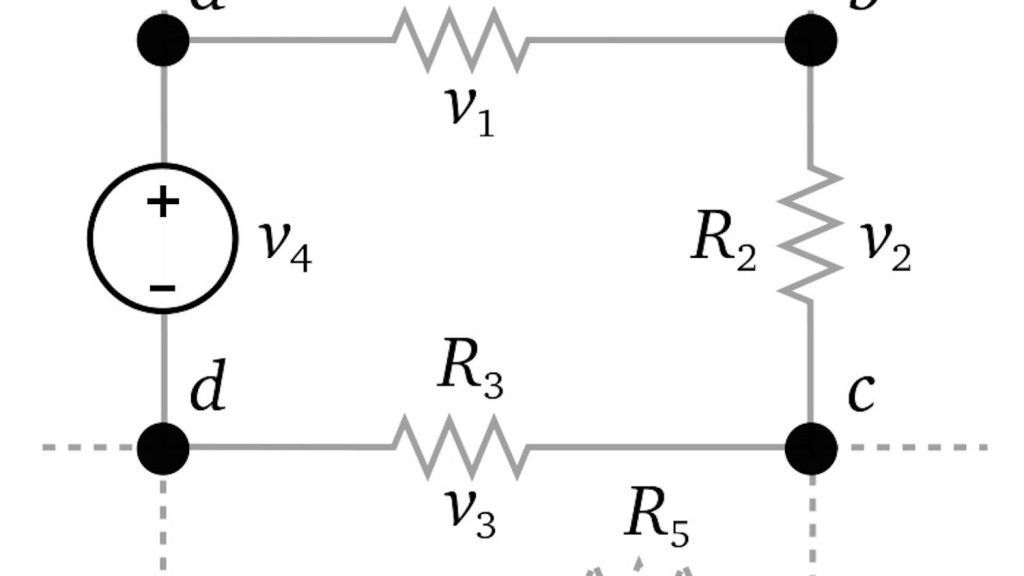
This law deals with voltages instead of current unlike the first law and hence is also known as Kirchhoff’s Voltage Law or Kirchhoff’s Mesh Law. It states that in a closed path or mesh, the algebraic sum of the products of currents and resistances of all conductors plus the algebraic sum of the emf’s is zero. Please note the word “algebraic” here, which simply means that not only does the quantity of these currents and voltages matter, but their direction as well. This leads us to the next question as to the determination of the sign of voltages and current in the closed mesh which is explained as follows.

Voltage – in case of a battery emf, a rise in voltage is given a +ve sign while a fall in voltage is given a –ve sign. This sign does not depend on the direction of current in that particular branch. On the contrary an IR drop over a resistor depends solely on the direction of current independently of any emf present in the branch.

Current – choosing the direction of current for purposes of calculation using Kirchhoff’s law is mostly a matter of convenience and can be taken either clockwise or anticlockwise BUT once a direction has been chosen, it must be stuck to, otherwise it will lead to confusion and wrong calculations.