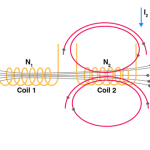
This is an important factor to be known for calculating Mutual inductance of two coils. Let us consider two nearby coils of N1 and N2 turns respectively.
The current through first coil i1 produces some flux Ψ1. The amount of magnetic flux linkages is understood by weber-turns.
Let the amount of magnetic flux linkage to the second coil, due to unit current of i1 be
N2φ1i1N2φ1i1
This can be understood as the Co-efficient of Mutual inductance, which means
M=N2φ1i1M=N2φ1i1
Hence the Co-efficient of Mutual inductance between two coils or circuits is understood as the weber-turns in one coil due to 1A of current in the other coil.
If the self-inductance of first coil is L1, then
L1i1=N1φ1=>L1N1φ1i1L1i1=N1φ1=>L1N1φ1i1
M=N2L1N1M=N2L1N1
Similarly, coefficient of mutual inductance due to current i2 in the second coil is
M=N1φ2i2⋯⋯⋯⋯1M=N1φ2i2⋯⋯⋯⋯1
If self-inductance of second coil is L2
L2i2=N2φ2L2i2=N2φ2
L2N2=φ2i2L2N2=φ2i2
Therefore,
M=N1L2N2⋯⋯⋯⋯2M=N1L2N2⋯⋯⋯⋯2
Multiplying 1 and 2, we get
M×M=N2L1N1×N1L2N2M×M=N2L1N1×N1L2N2
M2=L1L2=>M=L1L2−−−−√M2=L1L2=>M=L1L2
The above equation holds true when the whole changing flux of primary coil links with the secondary coil, which is an ideal case. But in practice, it is not the case. Hence, we can write as
M≠L1L2−−−−√M≠L1L2
andML1L2−−−−√=K≠1andML1L2=K≠1
Where K is known as the coefficient of coupling.
The Coefficient of coupling K can be defined as the ratio of actual coefficient of mutual inductance to the ideal (maximum) coefficient of mutual inductance.
If the value of k is near to unity, then the coils are said to be tightly coupled and if the value of k = 0, then the coils are said to be loosely coupled.
Applications of Inductors
There are many applications of Inductors, such as −
· Inductors are used in filter circuits to sense high-frequency components and suppress noise signals
· To isolate the circuit from unwanted HF signals.
· Inductors are used in electrical circuits to form a transformer and isolate the circuits from spikes.
· Inductors are also used in motors.