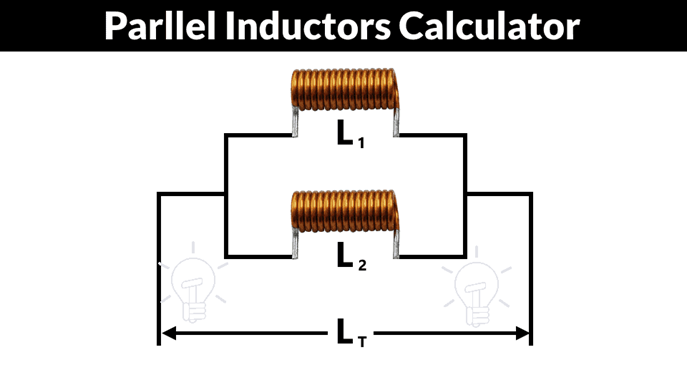
Let us observe what happens, when few resistors are connected in Parallel. Let us consider three resistors with different values, as shown in the figure below.

Inductance

The total inductance of a circuit having Parallel resistors is calculated differently from the series inductor network method. Here, the reciprocal (1/R) value of individual inductances are added with the inverse of algebraic sum to get the total inductance value.

Total inductance value of the network is

1LT=1L1+1L2+1L31LT=1L1+1L2+1L3

Where L₁ is the inductance of 1^st inductor, L₂ is the inductance of 2^ndinductor and L₃ is the inductance of 3^rd inductor in the above network.

From the method we have for calculating parallel inductance, we can derive a simple equation for two-inductor parallel network. It is

LT=L1×L2L1+L2LT=L1×L2L1+L2

Voltage

The total voltage that appears across a Parallel inductors network is same as the voltage drops at each individual inductances.

The Voltage that appears across the circuit

V=V1=V2=V3V=V1=V2=V3

Where V₁ is the voltage drop across 1^st inductor, V₂ is the voltage drop across 2^nd inductor and V₃ is the voltage drop across 3^rd inductor in the above network. Hence the voltage is same at all the points of a parallel inductor network.

Current

The total amount of current entering a Parallel inductive network is the sum of all individual currents flowing in all the Parallel branches. The inductance value of each branch determines the value of current that flows through it.

The total Current through the network is

I=I1+I2+I3I=I1+I2+I3

Where I₁ is the current through the 1^st inductor, I₂ is the current through the 2^nd inductor and I₃ is the current through the 3^rd inductor in the above network.

Hence the sum of individual currents in different branches obtain the total current in a parallel network.