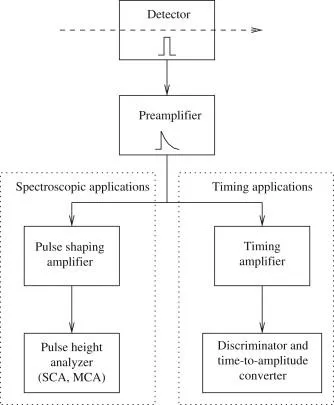
Signal processing plays an extremely important role in extracting useful information from detectors. Generally speaking, two pieces of information are important with respect to detection and measurement of radiation: the amplitude and the timing of the output pulse. Amplitude information is important with respect to applications, such as energy spectroscopy, in which measurement of the energy deposited by the incoming radiation is desired. On the other hand, there are applications, such as particle tracking, in which precise timing of pulses is required. In order to extract such information from narrow-width and low-amplitude detector pulses, a number of analog and digital signal processing (DSP) steps are required. Broadly speaking, either the signal can be processed entirely through a chain of analog circuitry or it can be converted to digital form for analysis. We will refer to the former in this book as analog signal processing. With the advent of cost-effective computing, DSP is now gaining a lot of popularity. In fact, it is now a method of choice wherever possible. It should, however, be noted that DSP does not eliminate the need for analog circuitry in the electronics chain. Some analog units are always needed to amplify the signal and make it usable for analog-to-digital converters (ADC). For example, although the availability of very fast ADCs (called flash ADCs) has made it possible to replace the pulse shaping step by a digital process, preamplifiers are still needed. Figure 8.0.1 shows analog and DSP steps that are generally adapted in detection systems.
What Is “Signal Processing” and Why Do We Do It?
As previously mentioned, signal processing condenses measurements to extract information about some distant state of nature. Signal processing can be described from different perspectives. To an acoustician, it is a tool to turn measured signals into useful information. To a sonar designer, it is one part of a sonar system. To an electrical engineer, it is often restricted to digitization, sampling, filtering, and spectral estimation. A modern underwater acoustic signal processing system can include the following.
•
Digitization (sampling in time and quantizing in amplitude)
•
Band-pass and base-band filtering
•
Beamforming (spatial filtering)
•
Matched filtering and/or incoherent integration
•
Detection, classification, localization, and tracking
Although measurements are typically acquired jointly in space and time, signal processing is usually partitioned to combine signals across space first and then time. The other components are similarly separable, in part owing to their inherent modularity and also from a paced evolution in computational power. For example, early deployment of beamformers required special hardware so only beam-output data were easily accessible for analysis. Easy access to data enabled advances in the modern signal processing components of detection, classification, localization, and tracking.
A broader view of modern signal processing can be found by considering its theoretical foundations, which come from mathematical statistics. Almost all underwater acoustics applications can be categorized as statistical inference, which is comprised of estimation and hypothesis testing . These two branches of statistical inference provide the mathematical framework and tools to derive or design signal processing algorithms extracting the desired information. Examples of point estimation include inferring depth via the depth sounder, internal-wave amplitude, or location of a mine on the seafloor. Hypothesis testing is itself a type of estimation where the state of nature is represented as a finite set (e.g., types of mines or marine mammal vocalizations). The most common is the binary hypothesis test known as a signal detection problem, for which the state of nature is the presence or absence of an object, phenomenon, or condition. For example, is there a fish school present or not? Is there a communications signal in the measurement or not? Are internal waves present or not? Most underwater acoustics applications combine both detection and estimation: is there a fish school and if so what type are they and how many fish are there in the school.
Each of the signal processing components in the above-mentioned list (perhaps excluding digitization) can be derived through either a detection or estimation paradigm. The importance of casting signal processing as a detection or estimation problem comes from the structured design approaches available within the field of mathematical statistics. The design approaches provide a means for algorithm derivation and dictate when and what optimality criteria are satisfied or if the resulting algorithm is suboptimal. For example, the losses incurred in performing the signal processing operations sequentially as opposed to in a unified manner can be evaluated or unified algorithms can be derived (e.g., see Ref. [3] for combined beamforming and tracking).
Representing signal processing functions as detection or estimation problems has the added benefit of providing unambiguous performance metrics. Early signal processing development and analysis relied on SNR or a similar measure called deflection as the primary performance metric. Because these metrics are derived from second-order statistics of the signal envelope (i.e., average power), they are an unambiguous representation of performance only under certain conditions (e.g., Gaussian-distributed noise). It is important to note the sonar equation is similarly a second-order statistical performance metric and therefore may not accurately represent performance in all scenarios.