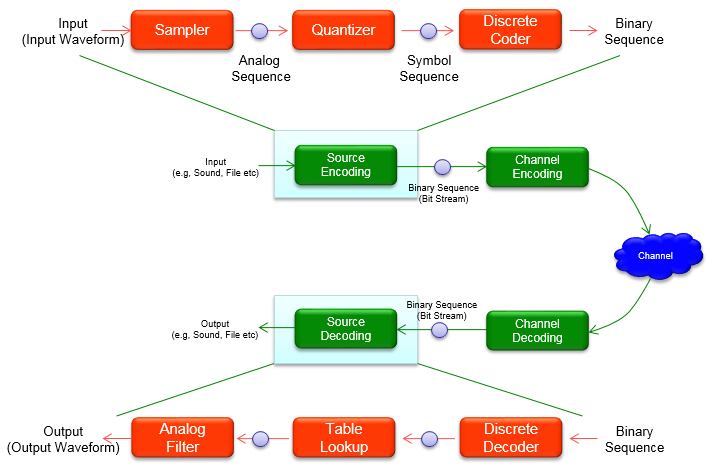
As described in Source encoding, one purpose of the source encoder is to eliminate redundant binary digits from the digitized signal. The strategy of the channel encoder, on the other hand, is to add redundancy to the transmitted signal—in this case so that errors caused by noise during transmission can be corrected at the receiver. The process of encoding for protection against channel errors is called error-control coding. Error-control codes are used in a variety of applications, including satellite communication, deep-space communication, mobile radio communication, and computer networking.

There are two commonly employed methods for protecting electronically transmitted information from errors. One method is called forward error control (FEC). In this method information bits are protected against errors by the transmitting of extra redundant bits, so that if errors occur during transmission the redundant bits can be used by the decoder to determine where the errors have occurred and how to correct them. The second method of error control is called automatic repeat request (ARQ). In this method redundant bits are added to the transmitted information and are used by the receiver to detect errors. The receiver then signals a request for a repeat transmission. Generally, the number of extra bits needed simply to detect an error, as in the ARQ system, is much smaller than the number of redundant bits needed both to detect and to correct an error, as in the FEC system.

Repetition codes

One simple, but not usually implemented, FEC method is to send each data bit three times. The receiver examines the three transmissions and decides by majority vote whether a 0 or 1 represents a sample of the original signal. In this coded system, called a repetition code of block-length three and rate one-third, three times as many bits per second are used to transmit the same signal as are used by an uncoded system; hence, for a fixed available bandwidth only one-third as many signals can be conveyed with the coded system as compared with the uncoded system. The gain is that now at least two of the three coded bits must be in error before a reception error occurs.

The Hamming code

Another simple example of an FEC code is known as the Hamming code. This code is able to protect a four-bit information signal from a single error on the channel by adding three redundant bits to the signal. Each sequence of seven bits (four information bits plus three redundant bits) is called a code word. The first redundant bit is chosen so that the sum of ones in the first three information bits plus the first redundant bit amounts to an even number. (This calculation is called a parity check, and the redundant bit is called a parity bit.) The second parity bit is chosen so that the sum of the ones in the last three information bits plus the second parity bit is even, and the third parity bit is chosen so that the sum of ones in the first, second, and fourth information bits and the last parity bit is even. This code can correct a single channel error by recomputing the parity checks. A parity check that fails indicates an error in one of the positions checked, and the two subsequent parity checks, by process of elimination, determine the precise location of the error. The Hamming code thus can correct any single error that occurs in any of the seven positions. If a double error occurs, however, the decoder will choose the wrong code word.

Convolutional encoding

The Hamming code is called a block code because information is blocked into bit sequences of finite length to which a number of redundant bits are added. When k information bits are provided to a block encoder, n − k redundancy bits are appended to the information bits to form a transmitted code word of n bits. The entire code word of length n is thus completely determined by one block of k information bits. In another channel-encoding scheme, known as convolutional encoding, the encoder output is not naturally segmented into blocks but is instead an unending stream of bits. In convolutional encoding, memory is incorporated into the encoding process, so that the preceding M blocks of k information bits, together with the current block of k information bits, determine the encoder output. The encoder accomplishes this by shifting among a finite number of “states,” or “nodes.” There are several variations of convolutional encoding, but the simplest example may be seen in what is known as the (n,1) encoder, in which the current block of k information bits consists of only one bit. At each given state of the (n,1) encoder, when the information bit (a 0 or a 1) is received, the encoder transmits a sequence of n bits assigned to represent that bit when the encoder is at that current state. At the same time, the encoder shifts to one of only two possible successor states, depending on whether the information bit was a 0 or a 1. At this successor state, in turn, the next information bit is represented by a specific sequence of n bits, and the encoder is again shifted to one of two possible successor states. In this way, the sequence of information bits stored in the encoder’s memory determines both the state of the encoder and its output, which is modulated and transmitted across the channel. At the receiver, the demodulated bit sequence is compared to the possible bit sequences that can be produced by the encoder. The receiver determines the bit sequence that is most likely to have been transmitted, often by using an efficient decoding algorithm called Viterbi decoding (after its inventor, A.J. Viterbi). In general, the greater the memory (i.e., the more states) used by the encoder, the better the error-correcting performance of the code—but only at the cost of a more complex decoding algorithm. In addition, the larger the number of bits (n) used to transmit information, the better the performance—at the cost of a decreased data rate or larger bandwidth.

Coding and decoding processes similar to those described above are employed in trellis coding, a coding scheme used in high-speed modems. However, instead of the sequence of bits that is produced by a convolutional encoder, a trellis encoder produces a sequence of modulation symbols. At the transmitter, the channel-encoding process is coupled with the modulation process, producing a system known as trellis-coded modulation. At the receiver, decoding and demodulating are performed jointly in order to optimize the performance of the error-correcting algorithm.