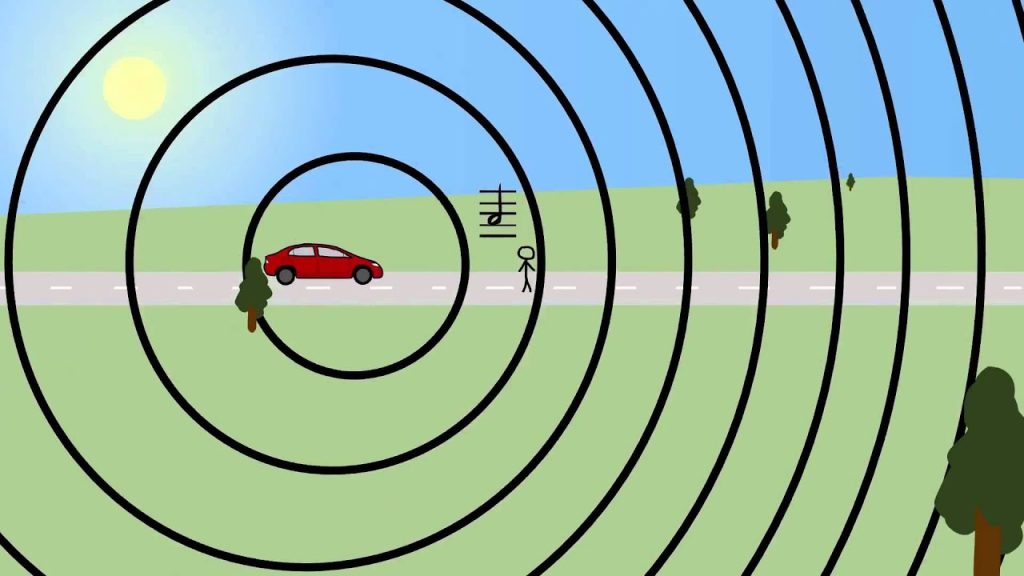
When the source of a wave moves relative to an observer, the observer notices a change in the frequency of the wave. This change is called the Doppler effect, after its discoverer, Austrian physicist Christian Doppler.

Doppler shiftDoppler shift.
Consider a source emitting a wave such as light or sound of frequency ν moving away from an observer at velocity v. The successive crests of the light waves will reach the observer at longer intervals than if the observer were at rest, and calculation shows that the observer will receive them with a frequency ν(1−v/c), where c is the velocity of the wave. The frequency of the wave will appear to the observer slightly lower than it would if the source were at rest. If the source is approaching, the frequency will be higher.
In sound this effect is an everyday experience; when a blowing horn is passed on the highway, the observer may notice that the pitch of the note seems to change. The Doppler effect for light waves is evident in spectroscopy. A shift to higher frequencies is called a blueshift, and a shift to lower frequencies is called a redshift. The redshifted light from other galaxies is evidence of the expansion of the universe.
Standing Waves
If a wave is confined to a closed space, it undergoes both reflection and interference. For example, consider a tube of length l. A disturbance anywhere in the air in the tube will be reflected from both ends and produce in general a series of waves traveling in both directions along the tube. From the geometry of the situation and the finite constant value of acoustic velocity, these must be periodic waves with frequencies fixed by the boundary conditions at the end of the tube. The allowed frequencies of the waves in the tube satisfy sin kl = 0; i.e., the allowed frequencies are ν = nv/2l, where n is any integer and v is the acoustic velocity in the tube. These are the frequencies of harmonic waves that can exist in the tube and still satisfy the boundary conditions at the ends. They are called the characteristic frequencies or normal modes of vibration of the air column. The fundamental frequency (n = 1) is ν = v/2l.
The higher frequencies, called harmonics or overtones, are multiples of the fundamental. It is customary to refer to the fundamental as the first harmonic; n = 2 gives the second harmonic or first overtone, and so on. Approximately the same set of characteristic frequencies hold for a cylindrical tube open at both ends, though the boundary conditions are different.
There are positions in the tube at which the displacement of the air is zero at all times. This cannot take place in a progressive wave; thus, the wave disturbance corresponding to a normal mode is known as a standing wave. The positions of continuous zero displacement are known as nodes, while the positions for which there is maximum displacement are called antinodes. The distance between successive nodes is equal to a half wavelength of the particular mode.