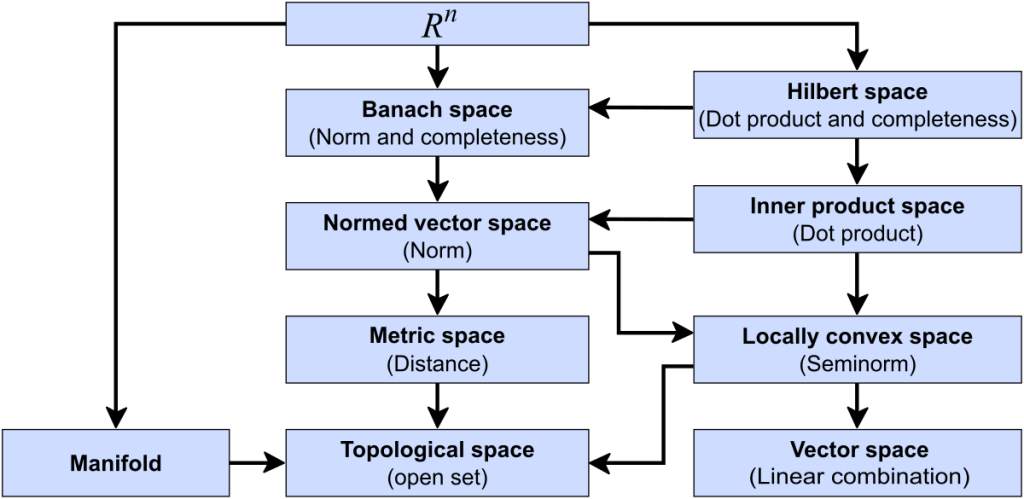
Sets of objects (vectors, sequences, polynomials, functions, etc.) often have certain special mappings defined on them that turn these sets into what are commonly called function spaces. Loosely speaking, functional analysis is about the properties of function spaces. Generally speaking, numerical computation problems are best handled by treating them in association with suitable mappings on well-chosen function spaces. For our purposes, the three most important special types of mappings are (1) metrics, (2) norms, and (3) inner products. You are likely to be already familiar with special cases of these really very general ideas. The vector dot product is an example of an inner product on a vector space, while the Euclidean norm (i.e., the square root of the sum of the squares of the elements in a real-valued vector) is a norm on a vector space. The Euclidean distance between two vectors (given by the Euclidean norm of the difference between the two vectors) is a metric on a vector space. Again, loosely speaking, metrics give meaning to the concept of “distance” between points in a function space, norms give a meaning to the concept of the “size” of a vector, and inner products give meaning to the concept of “direction” in a vector space.
We expressed interest in the sizes of errors, and so naturally the concept of a norm will be of interest. Later we shall see that inner products will prove to be useful in devising means of overcoming problems due to certain sources of error in a computation. In this section we shall consider various examples of function spaces, some of which we will work with later on in the analysis of certain computational problems. We shall see that there are many different kinds of metric, norm, and inner product. Each kind has its own particular advantages and disadvantages as will be discovered as we progress through the book.
Sometimes a quantity cannot be computed exactly. In this case we may try to estimate bounds on the size of the quantity. For example, finding the exact error in the truncation of a series may be impossible, but putting a bound on the error might be relatively easy. In this respect the concepts of supremum and infimum can be important. These are defined as follows,,

Metrics and Metric Spaces
In mathematics an axiomatic approach is often taken in the development of analysis methods. This means that we define a set of objects, a set of operations to be performed on the set of objects, and rules obeyed by the operations. This is typically how mathematical systems are constructed. The reader (hopefully) has already seen this approach in the application of Boolean algebra to the analysis and design of digital electronic systems (i.e., digital logic). We adopt the same approach here. We will begin with the following definition.